1.1 Os Elementos da Programação

Para aprender qualquer linguagem de programação é preciso entender quais são as suas:

expressões primitivas (componentes básicos da linguagem, como números, strings e booleanos);
meios de combinação (mecanismos que combinam elementos para formar expressões mais complexas);
E os meios de abstração (os quais permitem dar nomes e manipular elementos compostos, como os dados, procedimentos e processos).

1.1.1 Expressmaquinaões,
1.1.2 Nomes e o Ambiente e
1.1.3 Avaliando Combinações
1.1.4 Procedimentos Compostos

Uma expressão é o meio usado para expressar algo para a máquina. Se quero expressar a valor dez, digito 10, se quero nomear uma expressão defino um nome para ela e depois o seu valor:


;; Dados simples
10      ;; Retorna 10
"Nome"  ;; Retorna "Nome"

;; Nomeando Dados (Variaveis)
;; (define <nome><dado> )
(define idade 20)       ;; Numero
(define nome "Fulano")  ;; String
(define amo-estudar #t) ;; Booleano
                        ;;(#t Verdade, #f Falso)

;; Chamando as Variaveis
idade       ;; Retorna 20
nome        ;; Retorna "Fulano"
amo-estudar ;; Retorna #t

São pelos meios de combinação que criamos procedimentos mais robustos, permitindo expressar conceitos mais complexos, vejamos:


;; Números inteiros
(define a 10)
(define b 5)

;; Operações aritméticas
(+ a b)  ;; Soma: 15
(- a b)  ;; Subtração: 5
(* a b)  ;; Multiplicação: 50
(/ a b)  ;; Divisão: 2

(* 10 (/ (- (+ a b) (- a b))  2));; Retorna 50

;; String
(define nome "Fulano")
(define sobrenome "de Tal")

;; Concatenando strings
(string-append nome " " sobrenome)  ;; Retorna "Fulano de Tal"

;; Expressões lógicas (Booleano)
;; Operador 'and'
(and #t #t)  ;; Retorna #t
(and #t #f)  ;; Retorna #f
(and #f #t)  ;; Retorna #f
(and #f #f)  ;; Retorna #f

;; Operador 'or'
(or #t #t)  ;; Retorna #t
(or #t #f)  ;; Retorna #t
(or #f #t)  ;; Retorna #t
(or #f #f)  ;; Retorna #f

;; Operador 'not'
(not #t)  ;; Retorna #f
(not #f)  ;; Retorna #t

;; Combinando Expressões Lógicas
(and (or #t #f) (not #f))  ;; Retorna #t

Para manipular expressões, expressões primitivas, meios de combinação como se fosse um único elemento, um objeto abstrato, é usado funções. As quais são uma entidade que recebe argumentos e retorna um valor:


;; A estrutura da função é:
;; (define (nome-da-função <parâmetro>)
;;    <corpo>)

;; Definindo uma função simples
(define (quadrado x)
  (* x x))

;; Usando a função
(quadrado 5)  ;; Retorna 25

A função quadrado recebe o parâmetro x e utiliza-se de meios de combinação para calcular o quadrado de um número qualquer representado pelo parâmetro x.

Outro tipo de função é a anônima, ou seja, uma função que não tem nome. Em Scheme, funções anônimas ou lambda são criadas usando a palavra-chave lambda. Elas são úteis para criar funções temporárias ou para passar funções como argumentos para outras funções:


;; Definindo uma função anônima. Estrutura:
;; ((lambda (<parâmetro>) (<corpo>)) <valor-do-parâmetro>)
((lambda (x) (* x x)) 3)  ;; Retorna 9

;; Usando lambda em uma função definida
(define quadrado (lambda (x) (* x x)))
(quadrado 3)  ;; Retorna 9

1.1.5 Modelo de Substituição para Aplicação de Procedimentos

O modelo de substituição é uma técnica que descreve a execução de funções como um processo de substituição, onde as chamadas de procedimento são substituídas por seus corpos, com os argumentos apropriados.


(define (square x)
    (* x x)) ;; Corpo
      
(square 3) ;; Chamada

O modelo de substituição segue três passos principais:

Expansão (Substituição): A chamada do procedimento é substituída pelo seu corpo, trocando os parâmetros formais pelos valores dos argumentos.


;; Isso (square 3) é substituido por:
(* 3 3)

Redução (Avaliação): A expressão resultante é avaliada até se torne um valor.


;; Isso (* 3 3) retorna:
9

Encerramento: Quando o resultado é um valor atômico (exemplo: um número), o processo termina.

O modelo de substituição permite visualizar dois estilos de avaliação:

Avaliação Aplicativa (Applicative Order - "Eager"): Avalia primeiro os argumentos, depois substitui a função.
Avaliação Normal (Normal Order - "Lazy"): A função é expandida antes da avaliação dos argumentos.

Comparação com código


(define (square x)
(* x x))

;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;

;; #Applicative Order - "Eager"
;; Exemplo 1: Cálculo desnecessário

(square (+ 3 4))     ;; Chamada
→ (square 7)         ;; Primeiro avaliamos (+ 3 4)
→ (* 7 7)            ;; Agora substituímos o corpo
→ 49                 ;; Reduzimos para o resultado final

;; Aqui, avaliar (+ 3 4) antes faz sentido, pois será usado na função.

;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;

;; #Normal Order - "Lazy"
;; Exemplo 1: Cálculo adiado

(square (+ 3 4))       ;; Chamada
→ (* (+ 3 4) (+ 3 4))  ;; Primeiro substituímos a função sem avaliar os argumentos
→ (* 7 7)              ;; Agora avaliamos (+ 3 4), quando necessário
→ 49

;; Mesmo resultado, mas os argumentos foram avaliados apenas quando precisaram ser usados.


(define (choose-first x y)
  x)  ;; Apenas retorna x, ignorando y

;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;

;; #Applicative Order - "Eager"
;; Exemplo 2: Avaliação desnecessária

(choose-first 3 (* 1000 1000))  
→ (choose-first 3 1000000)  ;; Avaliamos (* 1000 1000) primeiro (mesmo sem precisar!)
→ 3                         ;; Apenas retorna x, então o cálculo foi inútil!

;; Aqui, o cálculo (* 1000 1000) foi feito mesmo sem necessidade!

;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;

;; #Normal Order - "Lazy"
;; Exemplo 2: Cálculo evitado

(choose-first 3 (* 1000 1000))  
→ 3  ;; Nunca avaliamos (* 1000 1000) porque o segundo argumento não foi usado!

;; Aqui, evitamos o cálculo desnecessário!


;; Exemplo 3: Erro inevitável
(choose-first 3 (/ 1 0))  ;; #Applicative Order - "Eager"
→ (choose-first 3 ERRO)   ;; Avalia (/ 1 0) antes → erro!
                          ;; Erro: Não se pode dividir por 0

;; Erro ocorre mesmo que y não seja usado!

;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;

(choose-first 3 (/ 1 0))  ;; #Normal Order - "Lazy"
→ 3                       ;; Nunca avaliamos (/ 1 0), então evitamos o erro!

;; Aqui, evitamos o cálculo desnecessário!

1.1.6 Expressões Condicionais e Predicados

...

Exercício 1.1: Resposta


10
;; 10

(+ 5 3 4)
;; 12

(- 9 1)
;; 8

(/ 6 2)
;; 3

(+ (* 2 4) (- 4 6))
;; 6 

(define a 3)
;; 

(define b (+ a 1))
;;

(+ a b (* a b))
;; 19

(= a b)
;; #f

(if (and (> b a) (< b (* a b)))
     b
     a)
;; 4

(cond ((= a 4) 6)
      ((= b 4) (+ 6 7 a))
      (else 25)) ;; 16
(+ 2 (if (> b a) b a))
;; 6

(* (cond ((> a b) a)
         ((< a b) b)
         (else -1))
   (+ a 1))
;; 16

Exercício 1.2: Resposta


(/ (+ 5 4 (- 2 (- 3 (+ 6 (/ 4 5)))))
   (* 3 (- 6 2) (- 2 7)))

Exercício 1.3: Resposta


(define (quadrado n)
  (* n n))

;; Solução 1
(define (maiores x y z)
  (if (or                     ;; x² + y²
        (and (= x y) (= y z)) ;; x = y = z {xy}
        (and (> y x) (> x z)) ;; y > x > z {xy}
        (and (> x y) (> y z)) ;; x > y > z {xy}
        (and (> y z) (= x y)) ;; x = y > z {xy}
      )
      (+ (quadrado x) (quadrado y))
      
  (if (or                      ;; z² + x²
        (and (> z x) (> x y))  ;; z > x > y  {xz}
        (and (> x z) (>= z y)) ;; x > z >= y {xz}
        (and (> x y) (= x z))  ;; z = x > y  {xz}
      ) 
      (+ (quadrado z) (quadrado x))
      
  (if (or                     ;; z² + y²
        (and (> z y) (>= y x)) ;; z > y >= x {yz}
        (and (> y z) (>= z x)) ;; y > z >= x {yz}
        (and (> y x) (= z y))  ;; z = y > x {yz}
      )
            (+ (quadrado z) (quadrado y))
            -1))))

;; Tudo diferente
(maiores 1 2 3) 
(maiores 1 3 2) 
(maiores 2 1 3) 
(maiores 2 3 1) 
(maiores 3 1 2) 
(maiores 3 2 1) 
;; Tudo igual
(maiores 1 1 1) 
;; Dois menores
(maiores 2 1 1)
(maiores 1 2 1)
(maiores 1 1 2)
;; Dois maiores
(maiores 1 2 2) 
(maiores 2 1 2) 
(maiores 2 2 1)

Exercício 1.4: Resposta


;; (define (a-plus-abs-b a b)
;;  ((if (> b 0) + -) a b))

(a-plus-abs-b a b) ;; Chamada
→ (                ;; Expansão
→ (if (> b 0)      ;; Expansão {Se b > 0 então:
→     +            ;; + se não:
→     -)           ;; -}
→ a b)             ;; Sendo b >  0 fica (+ a b)
                   ;; Sendo b <= 0 fica (- a b)

Exercício 1.5: Resposta


(test 0 (p))

;; Resposta
→  if (#t)    ;; 0 = 0
→  0          ;; Resultado
;; y             Essa parte nunca é chamada

1.1.7 Exemplo: Raízes Quadradas pelo Método de Newton

A Ciência da Computação é a arte de criar instruções eficazes (como fazer), diferindo-se da matemática, que busca verdades (o que é). Por exemplo:

Matemática: Define a raiz quadrada como $\sqrt{x} = y tal que y^{2} = x e y \geq 0$
Computação: Exige um procedimento para calcular y, como o método iterativo de Newton.

O método de Newton consiste em melhorar iterativamente uma estimativa até atingir precisão desejada:

Palpite Inicial: Comece com uma estimativa (ex: y = 1).
Iteração: Calcule a média entre y e x/y:
$y_{n o v o} = \frac{y + \frac{x}{y}}{2}$
Critério de Parada: Repita até ∣y² - x∣ < tolerância.

Implementação em Scheme (LISP):


;; Calcula o quadrado de um número
(define (quadrado x) 
  (* x x))

;; Define a média entre dois números
(define (media x y) 
  (/ (+ x y) 2))

;; Refina a estimativa usando o método de Newton
(define (melhora-estimativa estimativa x)
  (media estimativa (/ x estimativa)))

;; Verifica se a estimativa é suficientemente precisa
(define (estimativa-boa? estimativa x)
  (< (abs (- (quadrado estimativa) x)) 0.001))

;; Processo iterativo (recursivo) para busca da raiz
(define (raiz-iterativa estimativa x)
  (if (estimativa-boa? estimativa x)
      estimativa
      (raiz-iterativa (melhora-estimativa estimativa x) x)))

;; Função principal: inicia com estimativa = 1.0
(define (raiz x)
  (raiz-iterativa 1.0 x))

;; Exemplo: Raiz de 625 ≈ 25.0
(raiz 625)

Exercício 1.6: Resposta

O uso de new-if em sqrt-iter causa um loop infinito, pois a linguagem avalia todos os argumentos antes de aplicar new-if, executando a recursão mesmo quando o palpite já é bom o suficiente. O if original, como forma especial³, evita isso ao não avaliar o ramo não necessário.

Exercício 1.7: Resposta

O código estipula uma diferença entre o palpite e a raiz de um milésimo (1/100 ou 0,001), isso limita o código a achar raízes que se enquadre nessa limitação.
Quando os números são muito pequenos — próximos de 0 (zero) — a probabilidade de o retorno da raiz ser precoce por conta do ponto 1. é grande. Exemplo: A raiz quadrada de 0.0001 é 0.01, porém o código retorna 0.03230844833048122, uma diferença de 0,02230844833048122 (≈ 69,05%).
Agora quando com números muito grandes a situação 2. também pode ser aplicada, porém, só é relevante quando há casas decimeis em ordem de um décimo de milésimo (1/10000 ou 0,0001) de grandeza. Entretanto, quando há números a partir de quatorze casas decimais não retorna o resultado por falta de potência computacional.
Esse código funciona tanto para números grandes quanto pequenos:


(define (good-enough? guess next-guess)
  (<
    (abs (- guess next-guess ))
    (* guess 0.001))) ;; 0.1% de tolerância, poderia ser (/ guess 100)
;; A ideia é comparar o palpite novo com o antigo
;; caso a diferença for 1% então #t (true)

;; Restante do código para que a resposta funcione
(define (sqrt-iter guess x)
  ;; Com let crio uma variável local next-guess
  ;; para entrar como atributo em good-enough?
  ;; (let <variável> <valor>) ou
  ;; (let (<var1> <valor1>) (<var2> <valor2>))
  (let ((next-guess (improve guess x))) ;; Acrescentei a linha
    (if (good-enough? guess next-guess) ;; Alterei os atributos
        next-guess                      ;; Alterei o retorno
        (sqrt-iter next-guess x))))     ;; Alterei o atributo

(define (improvee guess x)
  (/ ( + guess (/ x guess)) 2)) ;; Simplifiquei

(define (sqrt x)
  (sqrt-iter 1.0 x))

;; (sqrt n) ;; Raiz quadrada de n

Exercício 1.8: Resposta


(define (good-enough? guess next-guess)
  (< (abs (- (square guess) next-guess))
      0.001)
)

(define (cube-root-iter guess next-guess) ;; Alterei o nome da função
  (let ((next-guess (improve guess x))))
  (if (good-enough? guess next-guess)
      next-guess
      (cube-root-iter next-guess x)
  )
)

(define (improve y x)              ;; Mudei o atributo guess por y
  (/ (+ (/ x (* y y)) (* 2 y)) 3)) ;; Mudei o corpo

(define (cube-root x) ;; Mudei o nome da função
  (cube-root-iter 1.0 x)
)

;; (cube-root n) ;; Raiz cubica de n

1.1.8 Procedimentos como Abstrações de Caixa Preta

A computação não lida com objetos reais, mas com objetos virtuais². Esses objetos são imaginados ou idealizados para representar conceitos e sistemas complexos de forma simplificada. Não há distinção significativa entre o que é possível construir e o que é possível imaginar, desde que se tenha o conhecimento necessário para transformar a ideia em realidade.

Abstração de caixa-preta é nada mais que uma técnica de abstração a qual simplifica a manipulação de sistemas complexos ao ocultar detalhes internos do funcionamento de um processo, expondo apenas suas interfaces: as entradas e saídas. Esse conceito facilita a compreensão, reutilização e ampliação de sistemas, permitindo que cada caixa seja tratada como uma unidade funcional:

Aqui, o método usado para calcular a raiz quadrada é abstraído como uma caixa-preta: você sabe o que entra e o que sai, mas não precisa entender os detalhes do cálculo.
A técnica permite que sistemas sejam escalados sem aumento significativo na complexidade. Por exemplo:
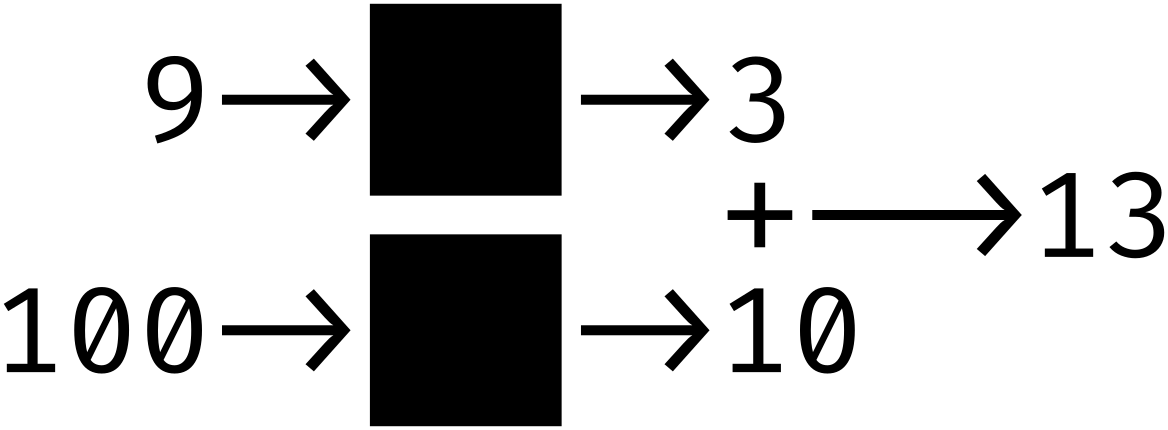
As caixas-pretas podem conter outras caixas-pretas.

² No contexto filosófico, o real e o virtual são formalizações que diferenciam o tangível do imaginário. Na ciência da computação, lidamos com sistemas idealizados, abstraídos e tratados como se estivessem numa "caixa mágica". Essa "caixa" é uma metáfora para sistemas computacionais que parecem possuir uma espécie de "espírito", capaz de executar as ideias previamente idealizadas e definidas por nós. Por meio dessas abstrações, é possível simplificar, organizar e manipular sistemas complexos, permitindo que o foco esteja em como esses objetos interagem e se comportam, em vez de nos detalhes técnicos de sua implementação interna.

³ Uma forma especial em Lisp (como if, cond, ou define) é uma construção sintática que não segue a avaliação padrão de procedimentos. Ela controla quando e como seus argumentos são avaliados. Por exemplo:

if avalia apenas um dos ramos (consequente ou alternativo), dependendo da condição.
Procedimentos ordinários, por outro lado, avaliam todos os argumentos antes de aplicar a função.

Em linguagens como Scheme, formas especiais são criadas usando macros. Macros são ferramentas de metaprogramação que operam em tempo de expansão de código (antes da execução). Elas transformam a estrutura sintática do código, permitindo que você defina novas regras de avaliação. Em linguagens como Python ou Java, não é possível criar formas especiais. Nelas, estruturas de controle (if, for, while) são fixas e definidas pelo núcleo da linguagem. Você só pode criar funções ordinárias, que avaliam todos os argumentos.